Because of the COVID-19 pandemic, people are missing important appointments because they are viewed as nonessential, possibly including children's pediatric dentist appointments. This study aims to determine how the COVID-19 pandemic has effected parents' willingness to allow children to visit pediatric dental practices and what safety measures would make them feel more comfortable visiting the dentist. The authors found a weak positive correlation between parents' unwillingness to allow their child to visit the dentist, however overall anxiety towards visiting the dentist during the pandemic was low.

The sequence of nitrogenous bases that make up the DNA of organisms can contain hidden mathematical sequences. Here the authors used BioPython, a programming tool, to find an organism that displays Gijswijt’s Sequence in its genome. In this manner they found that the common carp best displays Gijswijt’s Sequence in its genome.

In this study, the authors use existing mathematical models to how high school athletes pace 800 m, 1600 m, and 3200 m distance track events compared to elite athletes.

Alcohol use disorder is a chronic, relapsing disease that affects millions of Americans every day. There are limited treatment options for alcohol dependence and alcohol withdrawal symptoms, including depression and anxiety. Previous studies have shown that probiotics can decrease depression in rodents during maternal separation and anxiety in humans. Therefore, we hypothesized that the ethanol-withdrawn planaria who consumed probiotics would have decreased withdrawal symptoms as measured by increased motility compared to the ethanol-withdrawn planaria that were not fed probiotics. The ethanol-withdrawn planaria had a statistically significant decrease in motility compared to the control group, while the planaria that consumed probiotics had no statistically significant change in motility compared to the control group.

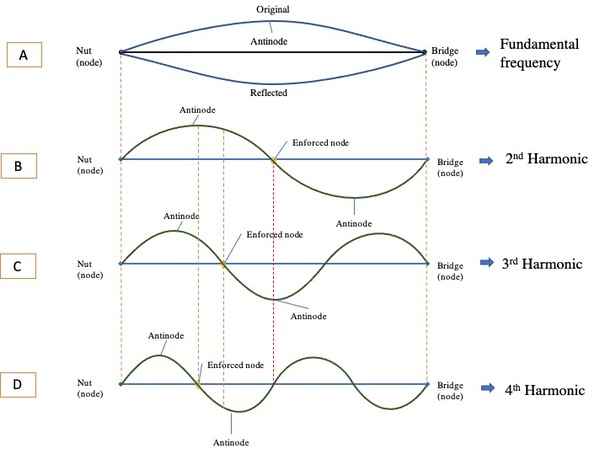
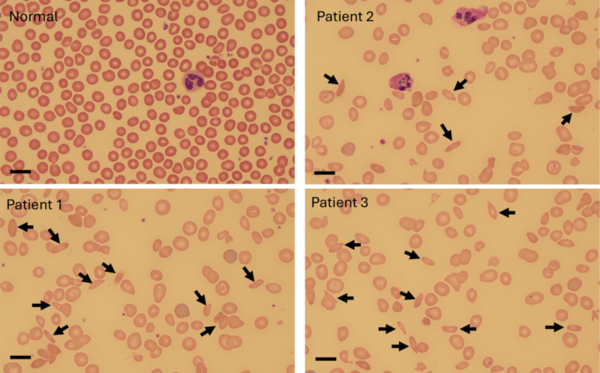
This study examines the higher harmonics in an oscillating string by analyzing the sound produced by a guitar with a spectrum analyzer. The authors mathematically hypothesized that the higher harmonics in the series of the directly excited 2^nd harmonic contain the alternate frequencies of the fundamental series, the higher harmonics of the directly excited 3^rd harmonic series contain every third frequency of fundamental series, and so on. To test the hypotheses, they enforced artificial nodes to excite the 2^nd, 3^rd, and 4^th harmonics directly, and analyzed the resulting spectrum to verify the mathematical hypothesis. The data analysis corroborates both hypotheses.

Here, recognizing the need to improve the efficiency of the conversion of solar energy to electrical energy, the authors used MATLAB to mathematically simulate a multi-layered thin film with an without an antireflective coating. They found that the use of alternating ZnO-SiO₂ multilayers enhanced the transmission of light into the solar cell, increasing its efficiency and reducing the reflectivity of the Si-Air interface.

In this study, the authors test whether a gravity vehicle, which is a vehicle powered by its own gravity on a ramp, could be designed to move faster when mathematical calculations for optimal mass and center of gravity were applied in the design.

These authors mathematically deduce a model that explains the interesting (and unintuitive) physical phenomenon that occurs when water falls.

Bubbles! In this study, the authors investigate the effects that different materials, temperature, and distance have on the formation of water bubbles on the surface of copper and steel. They calculated mathematical relations based on the outcomes to better understand whether interstitial hydrogen present in the d-block metals form hydrogen bonds with the water bubbles to account for the structural and mechanical stability.

In this work, the authors investigate the accuracy with which two different population growth models can predict population growth over time. They apply the Malthusian law or Logistic law to US population from 1951 until 2019. To assess how closely the growth model fits actual population data, a least-squared curve fit was applied and revealed that the Logistic law of population growth resulted in smaller sum of squared residuals. These findings are important for ensuring optimal population growth models are implemented to data as population forecasting affects a country's economic and social structure.