Browse Articles

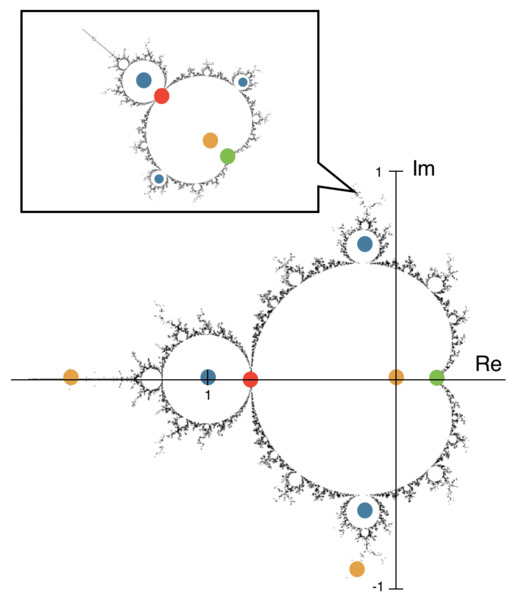
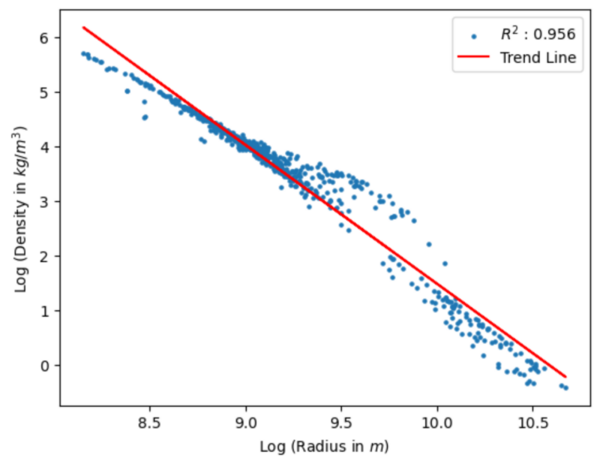
Here, beginning from an interest in fractals, infinitely complex shapes. The authors investigated the fractal object that results from crumpling a sheet of paper. They determined its fractal dimension using continuous Chi-squared analysis, thereby testing and validating their model against the more conventional least squares analysis.

This study aimed to predict and explain chaotic behavior in the Mandelbrot Set, one of the world’s most popular models of fractals and exhibitors of Chaos Theory. The authors hypothesized that repeatedly iterating the Mandelbrot Set’s characteristic function would give rise to a more intricate layout of the fractal and elliptical models that predict and highlight “hotspots” of chaos through their overlaps. The positive and negative results from this study may provide a new perspective on fractals and their chaotic nature, helping to solve problems involving chaotic phenomena.

Here based on an interest in fractals, the authors used a Julia Set Generator to consider a specific point on the Mandelbrot set with an associated coordinate. In this manner, they found that the complexity of the Mandelbrot and Julia Sets are governed by relatively simple rules, revealing that the intricate patterns of fractals can be defined by defined by simple rules and patterns.