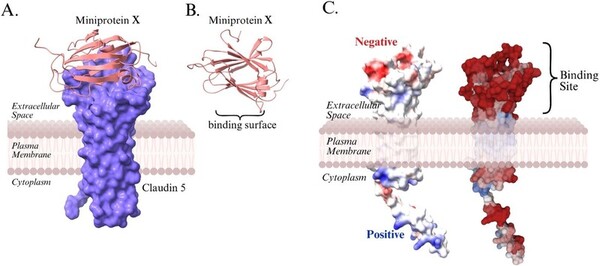
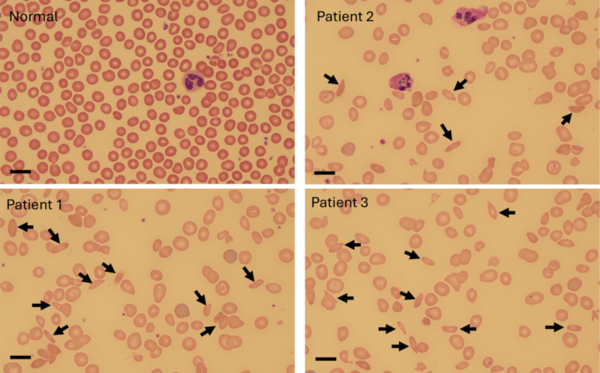
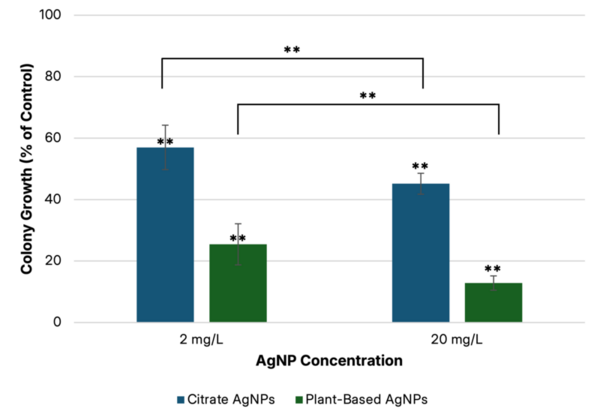
This paper looks at using spent coffee grounds as a partial substitute for titanium dioxide (TiO2) as a catalyst for chemical reactions. Using UV-Vis spectrophotometry, they found that adding the coffee grounds to TiO2 in a 3:1 ratio, there is still meaningful catalytic activity. This offers a cheaper solution than just using pure TiO2.
Read More...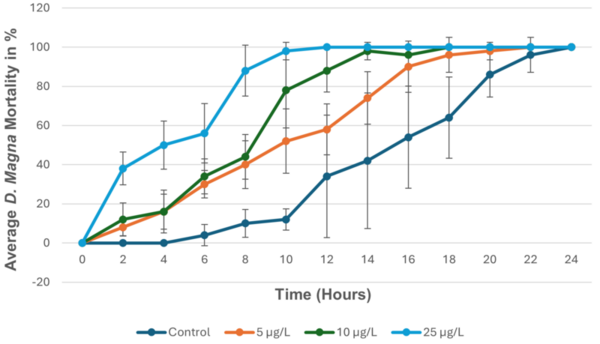
.png)