Modeling the moving sofas in circular hallways using geometric methods

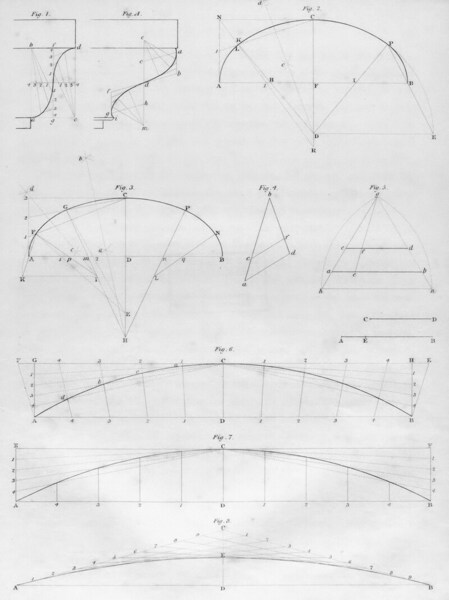
The moving sofa problem is an unresolved geometry problem introduced by Leo Moser in 1966. The problem seeks the largest planar and rigid shape that can move around a right-angled hallway of unit width. While the problem may seem like purely mathematical curiosity, it has many potential applications. Particularly, insights from the problem can be used to design trolleys that can move through tight corners or to navigate large objects in limited spaces. The more generalized piano mover’s problem also has practical applications in motion planning, such as robot navigation, robotic surgery, automation, driverless cars, and computer games. Though significant progress has been made in solving the original moving sofa problem, there has not been much study on more generalized cases. Here, we investigated the largest rigid shape that can be moved through a circular hallway of unit width with an arbitrary turn angle. We generated three hypotheses: first, the maximal area of moving sofa should depend on both the radius and the angle of the circular hallway; second, the maximal area should increase monotonically with the radius but decrease monotonically with the angle; and third, the result should resemble that of the original problem with turn angle θ = 90° and inner radius ri = 0. We found the results of our geometric models align well with the three hypotheses in both cases of inner radius ri = 0 and ri > 0. Our findings may provide new perspectives to applications of the moving sofa problem.