Solving a new NP-Complete problem that resembles image pattern recognition using deep learning
(1) Saint Mary's Catholic Academy
https://doi.org/10.59720/21-014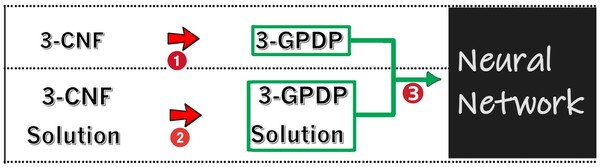
In computer science, non-deterministic polynomial time (NP) denotes the set of problems for which a solution, if it exists, can be checked quickly. We also call the set of problems in NP that are at least as hard as any other NP problem non-deterministic polynomial time complete (NP-complete). Although not known if they can be solved quickly as of writing this paper, NP-complete problems can be converted into one another quickly. A prominent and practical example is the protein folding problem, which is a problem of determining the shape and function of proteins. Some models of the protein folding problem have been shown to be NP-complete. In this paper, we discovered and provided a mathematical proof of a new NP-complete problem, that we named 3-Grid Pattern Decision Problem (3- GPDP). 3-GPDP is a decision problem that asks if a specific kind of pattern exists or not on a grid/matrix of numbers consisting of zeros and ones, much like image recognition. We hypothesized that a neural net would be able to solve 3-GPDP problems with high accuracy and low loss when trained. In support of our hypothesis, our experiment resulted in a neural net that performed with 84% accuracy and 0.14 loss without underfitting or overfitting. Moreover, there was also an increase in accuracy and decrease in loss with more training data. Hence, this further experimentally supported that using neural-networks can be a good heuristic approach to solve many NP-complete problems.
This article has been tagged with: