Browse Articles

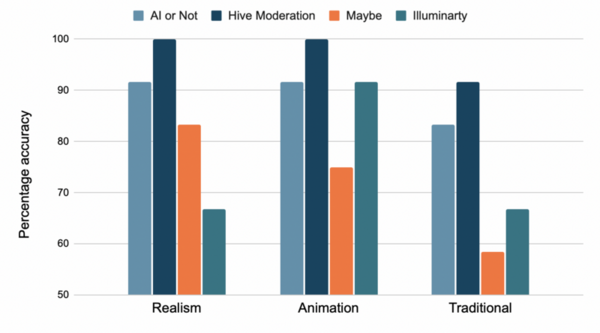
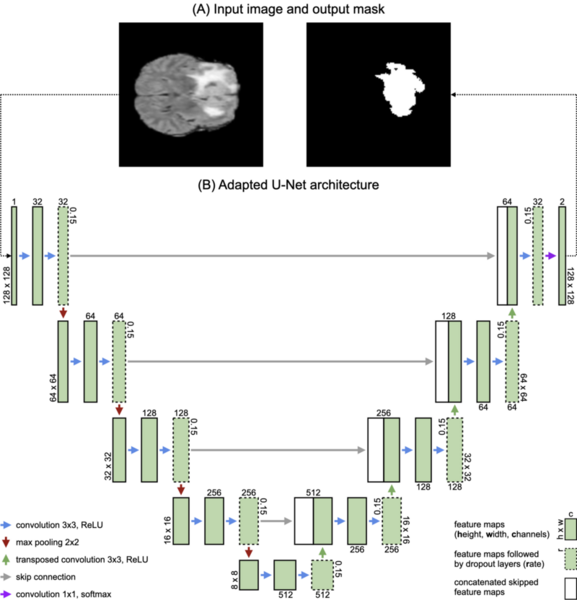
Here, the authors investigated the integration of large language models (LLMs) with drug target affinity predictors (DTAPs) to improve drug repurposing, demonstrating a significant increase in prediction accuracy, particularly with GPT-4, for psychotropic drugs and the sigma-1 receptor. This novel approach offers to potentially accelerate and reduce the cost of drug discovery by efficiently identifying new therapeutic uses for existing drugs.

Here, the authors used machine learning to analyze microscopic images of hair, quantifying various features to distinguish individuals, even within families where traditional DNA analysis is limited. The Discriminant Analysis (DA) model achieved the highest accuracy (88.89%) in identifying individuals, demonstrating its potential to improve the reliability of hair evidence in forensic investigations.

Here the authors sought to investigate whether and how cerebral stroke and other health-related variables are influenced together and amongst each other by using statistical analyses. Their analysis suggested relations between nearly all variables considered, with the strongest association between having heart disease and a cerebral stroke.

Droughts have a wide range of effects, from ecosystems failing and crops dying, to increased illness and decreased water quality. Drought prediction is important because it can help communities, businesses, and governments plan and prepare for these detrimental effects. This study predicts drought conditions by using predictable weather patterns in machine learning models.

Here seeking to develop a method to diagnose, hypertrophic cardiomyopathy which can cause sudden cardiac death, the authors investigated the use of a convolutional neural network (CNN) and long short-term memory (LSTM) models to classify cardiac magnetic resonance and heart electrocardiogram scans. They found that the CNN model had a higher accuracy and precision and better other qualities, suggesting that machine learning models could be valuable tools to assist physicians in the diagnosis of hypertrophic cardiomyopathy.

Skin cancer is a common and potentially deadly form of cancer. This study’s purpose was to develop an automated approach for early detection for skin cancer. We hypothesized that convolutional neural network-based models using transfer learning could accurately differentiate between benign and malignant moles using natural images of human skin.

Autism spectrum disorder (ASD) is hard to correctly diagnose due to the very subjective nature of diagnosing it: behavior analysis. Due to this issue, we sought to find a machine learning-based method that diagnoses ASD without behavior analysis or helps reduce misdiagnosis.

Middle school math forms the basis for advanced mathematical courses leading up to the university level. Large language models (LLMs) have the potential to power next-generation educational technologies, acting as digital tutors to students. The main objective of this study was to determine whether LLMs like ChatGPT, Bard, and Llama 2 can serve as reliable middle school math tutoring assistants on three tutoring tasks: hint generation, comprehensive solution, and exercise creation.

The authors investigate how well AI-detection machine learning models can detect real versus AI-generated art across different art styles.

This study compares the performance of two deep learning models, U-Net and DeconvNet, for segmenting gliomas from MRI scans.