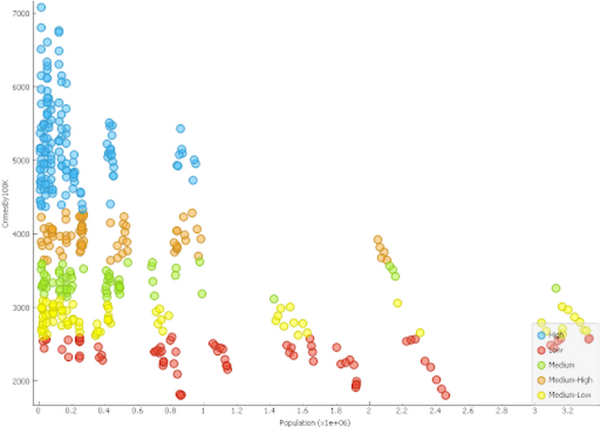
The authors look at using publicly available data and machine learning to see if they can develop a criminal activity index for counties within the state of California.
Read More...Implementing machine learning algorithms on criminal databases to develop a criminal activity index

The authors look at using publicly available data and machine learning to see if they can develop a criminal activity index for counties within the state of California.
Read More...Deep residual neural networks for increasing the resolution of CCTV images
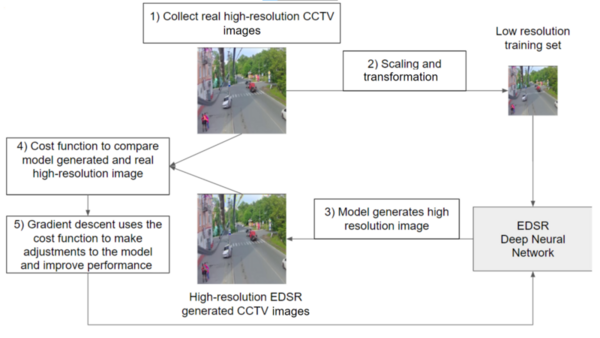
In this study, the authors hypothesized that closed-circuit television images could be stored with improved resolution by using enhanced deep residual (EDSR) networks.
Read More...Solving a new NP-Complete problem that resembles image pattern recognition using deep learning
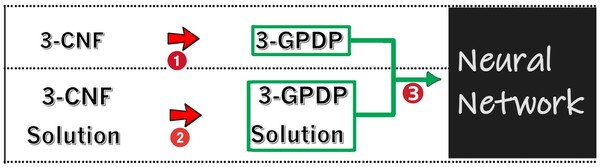
In this study, the authors tested the ability and accuracy of a neural net to identify patterns in complex number matrices.
Read More...An optimal pacing approach for track distance events

In this study, the authors use existing mathematical models to how high school athletes pace 800 m, 1600 m, and 3200 m distance track events compared to elite athletes.
Read More...An analysis of the feasibility of SARIMAX-GARCH through load forecasting

The authors found that SARIMAX-GARCH is more accurate than SARIMAX for load forecasting with respect to energy consumption.
Read More...The effect of COVID-19 on the USA house market
COVID-19 has impacted the way many people go about their daily lives, but what are the main factors driving the changes in the housing market, particular house prices?
Read More...Inflated scores on the online exams during the COVID-19 pandemic school lockdown

In this study, the authors explored whether students' test scores were significantly higher on online exams during the COVID-19 school lockdown when compared to those of the in-person exams before the lockdown.
Read More...Rubik’s cube: What separates the fastest solvers from the rest?

In this study, the authors assess the factors that allow some speedcubers to solve Rubik's Cubes faster than others.
Read More...Constructing an equally weighted stock portfolio based on systematic risk (beta)

In this article, the authors investigate whether stock selection across various sectors is efficient enough to outperform an overall market. Stocks from 2006 to 2020 were selected across sectors to calculate beta values using the Capital Asset Pricing Model.
Read More...Similarity Graph-Based Semi-supervised Methods for Multiclass Data Classification

The purpose of the study was to determine whether graph-based machine learning techniques, which have increased prevalence in the last few years, can accurately classify data into one of many clusters, while requiring less labeled training data and parameter tuning as opposed to traditional machine learning algorithms. The results determined that the accuracy of graph-based and traditional classification algorithms depends directly upon the number of features of each dataset, the number of classes in each dataset, and the amount of labeled training data used.
Read More...