Browse Articles

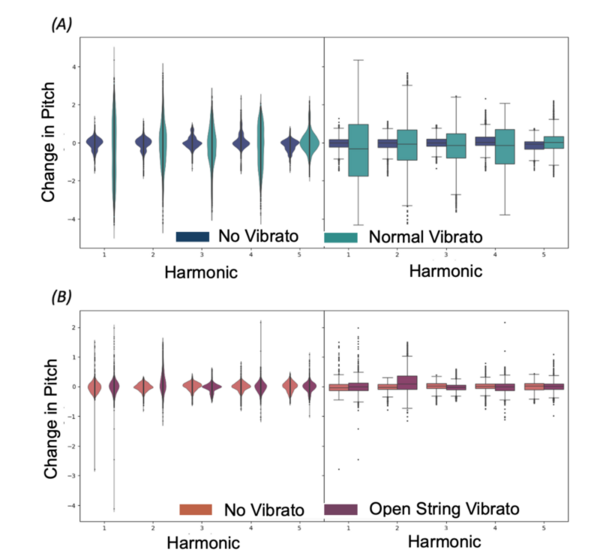
Vibrato, defined as a rapid and subtle oscillation in pitch, is a technique that is commonly used by musicians to add expression and colour to notes. However, on stringed instruments, there are certain notes (open string notes) on which it is impossible to perform the technique. Without vibrato, they can sound angular and unpleasant, especially when juxtaposed against other notes played with vibrato. String players therefore use an alternative to achieve the same vibrato effect on the open string — a technique referred to as “open string vibrato”. While the technique is widely used, it is unknown how much of a physical effect it has on the sound waves produced, if any at all. The purpose of this study is to analyse open string vibrato using a statistical approach to provide evidence to characterize the physical effect of the technique, and then compare it to normal vibrato. We hypothesised that it would have a noticeable and measurable effect on the sound waves produced because of the technique’s widespread usage. To test this, notes, with and without either open string vibrato or normal vibrato, were recorded on the violin. We analyzed the audio recordings using a computational and statistical approach. The results of the study partially agreed with our hypothesis: while the technique has an observable physical effect on the sound waves, the effect is weaker than expected. We concluded that open string vibrato does work, but has quite a subtle effect, and thus should only be used when there is no other option.

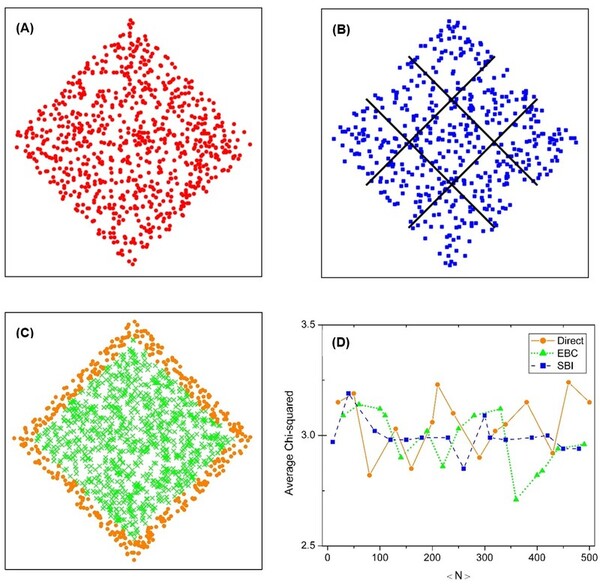
The causal set theory (CST) is a theory of the small-scale structure of spacetime, which provides a discrete approach to describing quantum gravity. Studying the properties of causal sets requires methods for constructing appropriate causal sets. The most commonly used approach is to perform a random sprinkling. However, there are different methods for sprinkling, and it is not clear how each commonly used method affects the results. We hypothesized that the methods would be statistically equivalent, but that some noticeable differences might occur, such as a more uniform distribution for the sub-interval sprinkling method compared to the direct sprinkling and edge bias compensation methods. We aimed to assess this hypothesis by analyzing the results of three different methods of sprinkling. For our analysis, we calculated distributions of the longest path length, interval size, and paths of various lengths for each sprinkling method. We found that the methods were statistically similar. However, one of the methods, sub-interval sprinkling, showed some slight advantages over the other two. These findings can serve as a point of reference for active researchers in the field of causal set theory, and is applicable to other research fields working with similar graphs.

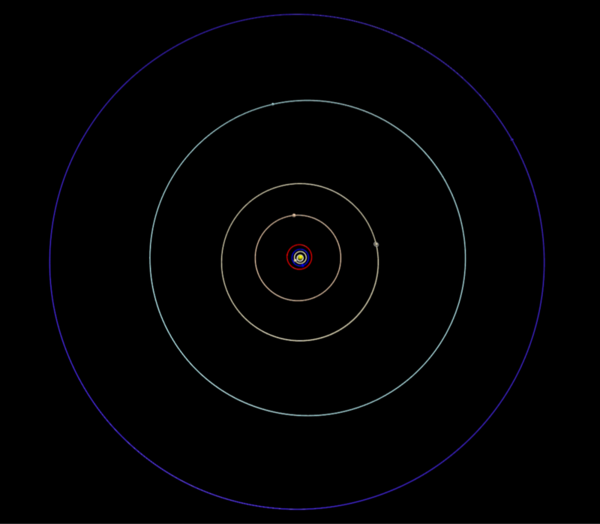
Someday, rockets from Earth may be launched towards worlds beyond our solar system. But will these rockets be able to reach their destination within a human lifetime? Ramaswamy and Giovinazzi simulate rocket launches to an Earth-like exoplanet to uncover whether it's physically possible to complete the journey within a lifetime.

Here the authors investigated the optical possibilities of gelatin and acrylic in regards to potential implementations at soft contact lenses. They fabricated lenses of different shapes and evaluated the refraction of laser light finding that gelatin needed to be thickened or increased in curvature to account for its lower refractive index compared to plastics, or used in a mixture to strengthen the lens.

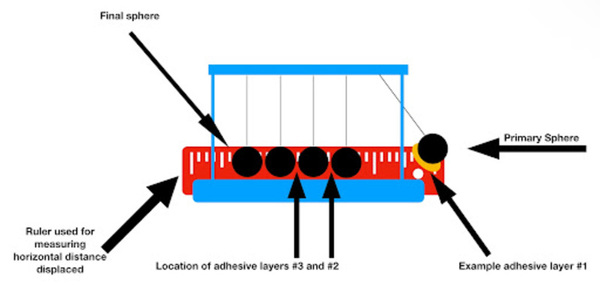
The energy conservation in a system of objects in collision depends on the elasticity of the objects and environmental factors such as air resistance. One system that relies heavily on elasticity is the Newton’s Cradle. We aimed to determine the extent to which these adhesives serve to mitigate or worsen the chaotic movements and elastic collisions.

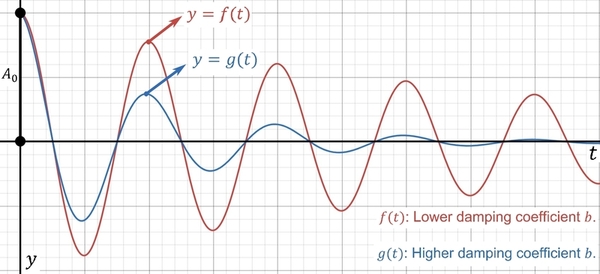
Dynamic viscosity is a quantity that describes the magnitude of a fluid’s internal friction or thickness. Traditionally, scientists measure this quantity by either calculating the terminal velocity of a falling sphere or the time a liquid takes to flow through a capillary tube. However, they have yet to conduct much research on finding this quantity through viscous damped simple harmonic motion. The present study hypothesized that the relationship between the dynamic viscosity and the damping coefficient is positively correlated.

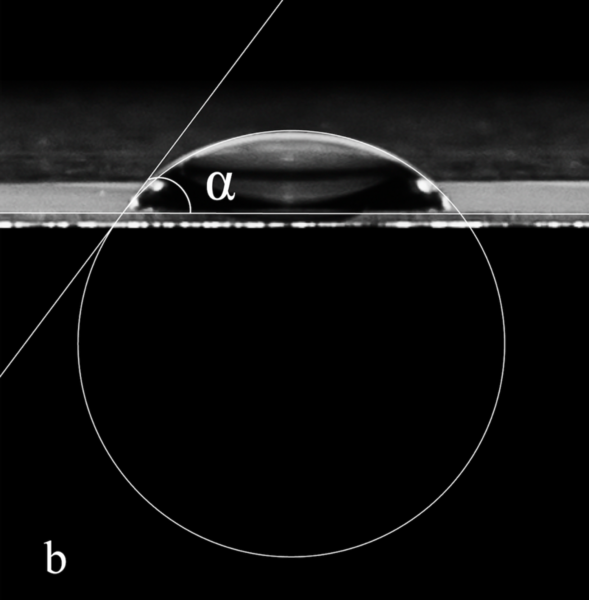
These authors mathematically deduce a model that explains the interesting (and unintuitive) physical phenomenon that occurs when water falls.

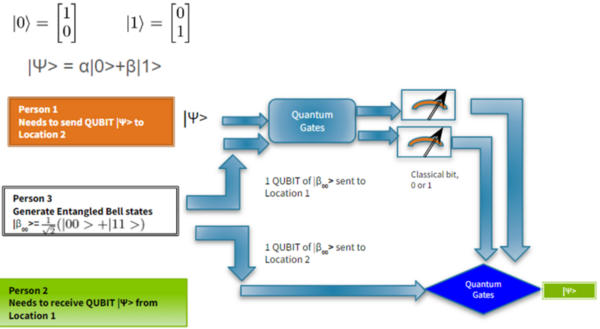
Quantum computers can perform computational tasks beyond the capability of classical computers, such as simulating quantum systems in materials science and chemistry. Quantum teleportation is the transfer of quantum information across distances, relying on entangled states generated by quantum computing. We sought to mitigate the error of quantum teleportation which was simulated on IBM cloud quantum computers.

Here, the authors sought to identify a method to optimize the lift generated by an airfoil based solely on its shape. By beginning with a Bernoullian model to predict an optimized wing shape, the authors then tested their model against other possible shapes by constructing them from Styrofoam and testing them in a small wind tunnel. Contrary to their hypothesis, they found their expected optimal airfoil shape did not result in the greatest lift generation. They attributed this to a variety of confounding variables and concluded that their results pointed to a correlation between airfoil shape and lift generation.

The authors explore how similar exoplanets are to Earth and whether they could be inhabited by humans and other living organisms.