The effect of Poisson sprinkling methods on causal sets in 1+1-dimensional flat spacetime

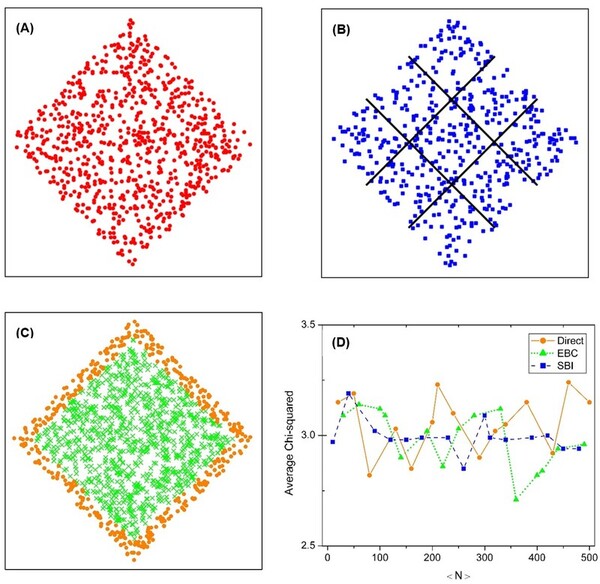
The causal set theory (CST) is a theory of the small-scale structure of spacetime, which provides a discrete approach to describing quantum gravity. Studying the properties of causal sets requires methods for constructing appropriate causal sets. The most commonly used approach is to perform a random sprinkling. However, there are different methods for sprinkling, and it is not clear how each commonly used method affects the results. We hypothesized that the methods would be statistically equivalent, but that some noticeable differences might occur, such as a more uniform distribution for the sub-interval sprinkling method compared to the direct sprinkling and edge bias compensation methods. We aimed to assess this hypothesis by analyzing the results of three different methods of sprinkling. For our analysis, we calculated distributions of the longest path length, interval size, and paths of various lengths for each sprinkling method. We found that the methods were statistically similar. However, one of the methods, sub-interval sprinkling, showed some slight advantages over the other two. These findings can serve as a point of reference for active researchers in the field of causal set theory, and is applicable to other research fields working with similar graphs.