Solving the Schrödinger equation computationally using the Lanczos algorithm

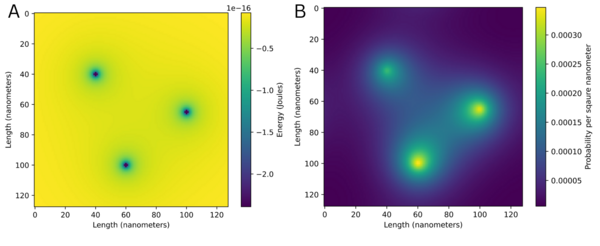
The Schrödinger equation is a fundamental equation in quantum mechanics that describes the behavior of particles in terms of wave functions. These wave functions provide a probabilistic description of where the particle is likely to be found, making them a crucial tool for understanding how particles interact with their environment. Methods for solving the Schrödinger equation analytically tend to be very mathematically complex, leading us to look for other ways to solve the Schrödinger equation. Unfortunately, in most cases, the Schrödinger equation cannot be solved for an exact solution. There are methods, however, for approximate solutions. In this paper, we investigated the Lanczos algorithm, a computational method that can solve the 2D Schrödinger equation in cases where finding an analytical solution would not be feasible. We discretized the Schrödinger equation, then ran a Python program using the Lanczos algorithm to solve for the ground state wave function. We hypothesized that the Schrödinger equation could be solved computationally for the ground state wave function using the Lanczos algorithm. We found that this method efficiently solved the Schrödinger equation for complicated 2D potentials. Additionally, we verified the accuracy of the method by comparing the results with wave functions from problems with known, exact solutions.