Heat conduction: Mathematical modeling and experimental data
(1) Shenzhen Senior High School, Shenzhen, China, (2) Department of Mathematics, North Carolina State University, North Carolina, (3) Unaffiliated author
https://doi.org/10.59720/21-108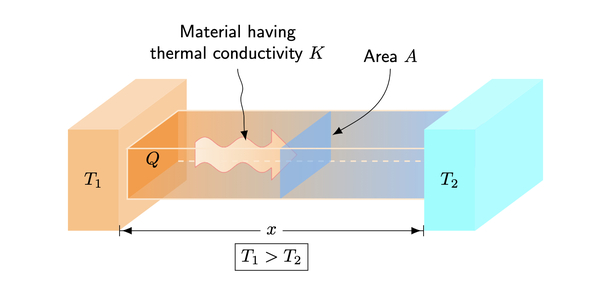
Mathematical models have been used to study and understand many biological and physical systems. However, for mathematical models to be useful, one needs to carefully assess the assumptions that go into the derivation of the mathematical model. For example, the heat equation, which is fundamental to the study of heat transfer, was derived based on an empirical rate formulation known as Fourier’s law of conduction and perfect insulation. Since perfect insulation is very difficult to implement in laboratory conditions, we hypothesized that the heat equation would produce a time course temperature solution that overestimates real temperature data as a consequence of heat loss to the surrounding air, which is not accounted for in the heat equation. To test this hypothesis, we derived two mathematical models for the rate of change of heat under two laboratory conditions: one that considers heat loss and one that does not. The experiment consists of a squared metal bar that was heated at one end by a soldering iron and the temperatures along its length were measured by thermocouples. Our results, when compared to experimental data, clearly demonstrated that the mathematical model obtained by taking into consideration the heat loss yielded a better fit to the experimental data than the model without the heat loss assumption. Specifically, the mathematical model with the assumption of perfect insulation overestimated the temperature data. The research findings showed that when using a mathematical model, it is important to examine carefully the assumptions made in deriving the mathematical model.
This article has been tagged with: